Pythagorean Theorem. Out of the blue?
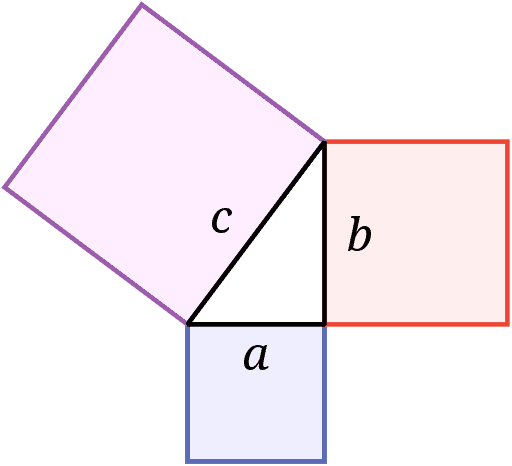
When I first heard the Pythagorean Formula, I wondered where did Pythagoras get the idea of that relationship? The teacher showed a right triangle and drew squares upon each side.
That was so unintuitive to me. It was a deduction after the fact. Although the drawing was explicit (Figure 1), it didn’t motivate my understanding of why the formula was valid or suggest a method for proving it.
Years later, I stumbled across a construction that makes much more sense. Consider a square (Figure 2). Divide a side anywhere into two parts, named a and b. Then from the first a draw a straight line to point a on the adjacent side. Do the same to the third side, the fourth side, then close the inscribed square by drawing a straight line from the fourth side to the original point a.
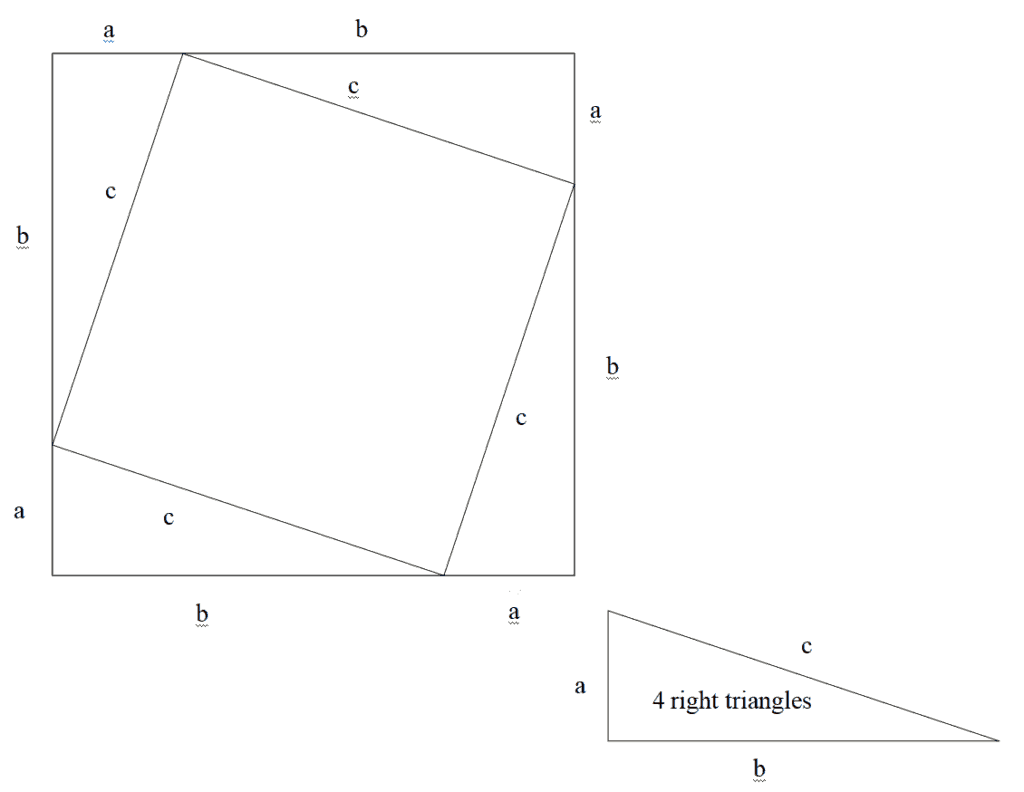
Figure 2 shows the original square of side a+b and the inscribed square of side c.Â
Area of original square = Area of inscribed square + 4* identical right triangles
(a + b)2 = c2 + 4(½ ab)
a2 + 2ab + b2 = c2 + 2 ab
a2 + b2 = c2
Perhaps some other teachers developed the inscribed square to explain the Pythagorean Theorem. I wish mine had.
Image Pythagorean Triangle with squares on each side. en:User:Wapcaplet, CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons