Gas Price Inflation
Update Apr 13, 2023. Nine years after this post, the price of gasoline averages $3.62. In 2013 the actual gas price was 3.53. It has risen at a rate of 0.3% yearly. Surprisingly low.
Got a chance to use Python for something I used to calculate in MathCad or Basic.
In a replay of a Twilight Zone episode (1960), “The Hitchhiker” a sign shows gas cost 32.9 cents/gal. Now, in 2014, it’s 10 times higher.
As a baby boomer, I’m used to cautions about considering the inflation rate in retirement planning, but there the idea is abstract.
What is the average rate of gas inflation over a period of 54 years to produce a ten-fold increase in price?
Answer: 4.4%
Inflation over the Years
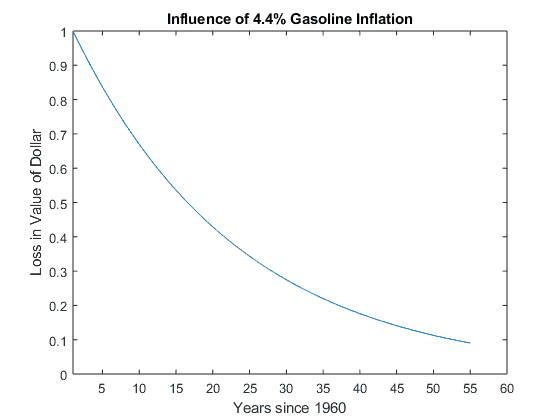
If all prices suffered from the same inflation as gasoline did, a dollar now would buy about 12% of what a dollar from 1960 did.
FYI. Dividing 72 by 4.4 yields 16 1/3 years, the # of years gas takes to double, if it increased smoothly at an average rate of 4.4%/year
Python code
import math
S = 32.9 # gas cost 32.9 cents in 1960 Twilight Zone ‘The Hitchhiker’
E = 329.0 # gas costs about $3.29 in 2014. Rounded down to make it 10 times earlier price
n = 54
above = math.log(E/S)/(n-1)
r = math.exp(above) -1
print(‘The average rate of gasoline inflation is’, ‘{0:3f}’.format(r))

