Ari Lox
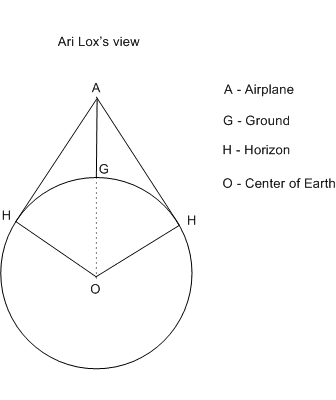
Arithophilus Loxodrome sat comfortably in the window seat of an intercontinental jet, thirty-one thousand one hundred and forty-three feet above the southernmost tip of the five freshwater lakes that were formed by the retreating glaciers of the Pleistocene Epoch. Ari wondered to what distance his natural ocular mechanism would perceive the horizon. What portion of this vast hydrated sphere, the third planet of a G type star, was available for his sensory contemplation?
A small cup full of coca, caffeine, caramel, sugar, and carbonic acid fizzed over a cube of frozen dihydrogen oxide while Ari pondered.
Owning a sharp pencil and a thick pad of yellow paper, Ari sipped his liquid resuscitative and attacked the problem in a manner befitting his high school geometry, where the text was expurgated Euclid from two thousand years ago. Well, maybe not his particular copy of the text.
Ari was pleased with his solution. He now knew that, while zipping above the jet stream and Chicago, his visual range extended from Green Bay, Wisconsin to Ann Arbor, Michigan. He could see the dual components of the Mid-West—the Iowa fields of grain to the home city of the Wright brothers, Dayton, Ohio.
Not long after, the pressure difference between the cabin and his inner ear notified our traveler that descent to his destination, that large conurbation of humans that populate the shores and littoral forests of the drowned estuary of the Susquehanna River, had commenced.
After the first euphoria of descent and geometric solution has passed, Ari thought, “That was too easy. I must elaborate.”
The stars had completed one-twelfth their daily cycle before Ari had time to consider the problem again.
How many square miles could he see from his satellite home, parked presently in its geostationary garage above the Amazon basin?
Ari is many things, but he is not enamored of calculations for the sake of calculations. Proud possessor of a calculating machine of immense power—one that Newton would have adored and that Pythagoras would have slaughtered sheep to—Ari translated his specific solution to a general algorithm that allowed our inquisitive investigator to solve the problem from the various heights he found interesting.

From atop the Washington Monument, one could espy the rolling hills of Manassas, where the battles of Bull Run in the American Civil War had been contested.
Noticing that the surface area he could see approached a limit as the view’s height above the Earth’s surface increased; Ari deduced that the value of the limit was one-half that of the Earth’s orb, as it should be.
Lastly, how strange that a rodent, that particularly pernicious metaphor for treachery and trickery, could see a third of a mile in Ari’s idealized world, where its line of sight was not obstructed by the vulgarity of reality.